А.Е.Старобинец

Заметка 7

О методе преломленных волн

Способы построения преломляющих границ

Из классических способов наиболее часто в практике интерпретации данных МПВ для построения преломляющих границ используются способы t0 (средних арифметических), сопряженных точек и полей времен.

В настоящее время главным образом применительно к данным малоглубинных сейсмических наблюдений широко используется сейсмическая томография на преломленных волнах.

Способ t0 (средних арифметических) основан на следующих допущениях: преломляющая граница на участке между критическими лучами преломленных волн, распространяющихся во встречных направлениях и приходящих в общую точку профиля с координатой x считается прямолинейной, а граничная скорость вдоль этого участка – постоянной (Рис.7_1а).

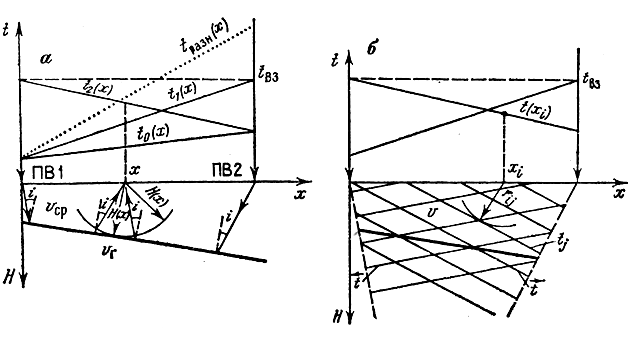
Рис.7_1. Схемы, поясняющие способы построения преломляющих сейсмических границ

 а – способ t0;      б – способ полей времен.

Для реализации способа должны быть известны граничная и средняя скорости.

Граничная скорость определяется по разностному годографу.

Глубина Н (х) по нормали к преломляющей границе определяется по формуле:

где i = arc sin (vcp/vг) – критический угол.

Преломляющая граница строится как огибающая окружностей радиусом Н(х) с центрами в точках х профиля.

Способ сопряженных точек основывается на том, что  сумма времен пробега преломленной волны по лучам, соответствующим сопряженным точкам (Рис.7_2), удовлетворяет равенству:

где 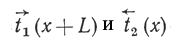– времена в сопряженных точках; L – расстояние между сопряженными точками.

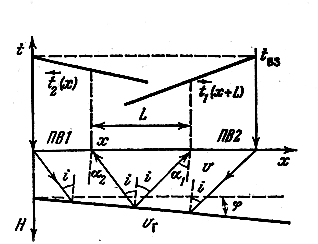
Рис.7_2. Схема, поясняющая способ сопряженных точек

 

Суть способа сопряженных точек состоит в том, что по заданной зависимости скорости от глубины восстанавливаются лучи преломленной волны для встречных годографов и находятся точки пересечения лучей, для которых выполняется условие (7.2). Такие точки пересечения и являются точками искомой преломляющей границы. Наиболее удобна численная реализация способа.

Граничная скорость определяется по формуле:

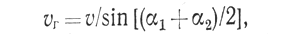
где v – скорость в покрывающей среде; и α1 и α2 углы выхода лучей, соответствующих паре сопряженных точек.

Способ сопряженных точек более трудоемок, чем способ t0, но применим для построения криволинейных преломляющих границ.

Способ полей времен наиболее универсальный и помехоустойчивый. Он применим для построения преломляющих границ произвольной формы, как в однородных, так и неоднородных средах, и позволяет при необходимости учитывать преломление лучей на промежуточных границах раздела. В его основе лежит последовательное восстановление фронтов (изохрон поля времен) преломленной волны в определенные моменты времени по встречным годографам в среде с известной скоростной зависимостью в соответствии с принципом Гюйгенса.

Если реализовать способ графическим путем, для восстановления изохрон поля времен, характеризуемых значениямии tj, нужно проводить дуги окружностей с центрами в точках на линии наблюдений и радиусами радиусами rji = v[t(xi)–tj], где t(xi)–время в точке xi на прямом или встречном годографе.

Затем находятся их огибающие (рис. 7_1, б). Они представляют собой искомые изохроны.

Поскольку сумма времен пробега преломленных волн от двух пунктов возбуждения до расположенной между ними произвольной точки преломляющей границы равна взаимному времени, то преломляющая граница находится как геометрическое место точек пересечения изохрон прямого и встречного полей времен, для которых удовлетворяется условие:

где tвз – взаимное время; 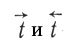– время прямой и обратной изохрон.

Если скорость распространения колебаний в покрывающей среде изменяется с глубиной, то положение фронта волны в заданные моменты времени при реализации способа графическим путем может быть определена с помощью лучевых диаграмм с изображенными на них изохронами.

В случае многослойной покрывающей среды для восстановления изохрон ниже каждой построенной (или априорно заданной) преломляющей границы центры окружностей совмещаются с точками ее пересечения с изохронами, восстановленными в покрывающей среде.

Для определения граничной скорости по полям времен cтроится годограф скользящей вдоль преломляющей границы волны: по оси абсцисс откладываются расстояния между точками пересечения построенной преломляющей границы с восстановленными изохронами любого из встречных полей, времен, а по оси ординат – время соответствующей изохроны. Кажущаяся скорость, определенная по такому годографу, равна искомой граничной скорости.

Для детального изучения характера изменения граничной скорости вдоль профиля и уменьшения влияния случайных погрешностей используется способ интервальных граничных скоростей. Значения vr определяются на малой базе ∆l, а затем сглаживаются в скользящем окне длиной d = (n–1)/∆l (n – число точек, по которым проводят сглаживание).

При численной реализации способа восстановление поля времен в дискретных точках среды осуществляется либо путем решения разностным методом нелинейного дифференциального уравнения в частных производных (уравнения эйконала) на прямоугольной или косоугольной сетке с краевыми условиями, определяемыми годографами преломленной волны, либо путем решения, базирующегося на аналитическом определении изохрон, в виде огибающей системы окружностей с центрами на линии наблюдений, которое формализует последовательность операций при ручной интерпретации.

Численные способы полей времен позволяют задавать закон изменения сейсмической скорости в виде произвольной функции v(x, z) и выполнять построения с использованием трехмерного временного поля.

Дифференциальное уравнение эйконала в прямоугольной системе координат имеет вид:

[dt (x, z)/dx]2 + [dt (x,.z)/dz]2=1/v2(x, z).                                                                                                                   (7.4)

В математической постановке построение сейсмической границы путем восстановления временного поля t(x, z) по наблюденному годографу Т(х) отвечает решению задачи Коши для уравнения (7.4) с начальным условием

t(x, 0) = T(х).                                                                                                                                                                  (7.5)

При прямоугольной сеточной аппроксимации уравнения (7.4) и условия (7.5) задача сводится к решению разностного уравнения для определения величины tJi в узлах сетки:

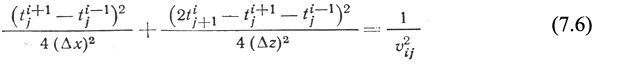
при условии, что t0i = Ti.

Из уравнения (7.6) следует, что время в узле сетки:

С помощью уравнения (7.7) определяются значения времен во всех узлах сеточной области.

Решение задачи на косоугольной сетке несколько сложнее.

Путем линейной интерполяции по узлам сетки находятся пары значений расчетного времени по прямому и встречному годографам. При этом координаты точек преломляющей границы определяются в соответствии с условием:

где t1z и t2z – значения времени на линии z = const, определенные по прямому и встречному годографам.

Для применения этого алгоритма годографы сложной формы, характеризующиеся резкими изменениями кажущейся скорости, должны быть предварительно сглажены.

В алгоритме, в котором формализованы операции графической реализации способа полей времен, предусмотрено два варианта нахождения изохрон.

Один базируется на аналитическом решении системы уравнений, определяющих координаты точек огибающих при постоянной скорости распространения волн в среде и горизонтальной поверхности наблюдений:

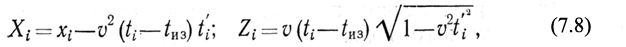
где Xi, Zi – координаты точки изохроны, соответствующей i-й точке годографа; xi ,ti – координаты i-й точки годографа; tиз – время изохроны; tиз’ – производная годографа t(x) в i-й точке; v – скорость в покрывающей среде.

Для определения производной ti’ годограф аппроксимируется кубическим сплайном. Это не изменяет положения изохроны, а приводит лишь к увеличению ее гладкости.

В другом варианте восстановления изохрон дифференцирование годографа не производится, что обеспечивает более устойчивое решение задачи.

Алгоритм основан на аналитическом определении координат точек пересечения окружностей. Абсцисса точки изохроны Хi , если абсциссы точек пересечения окружностей упорядочены, определяется как среднее значение между соседними абсциссами точек пересечения. В противном случае она определяется по формуле:

Xi = xi + v ( ti-tиз ).

Ордината точки изохроны Zi определяется как максимальное значение ординат близлежащих окружностей в точке с координатой Хi.

Абсциссы Хгр точек пересечения прямых и обратных изохрон, удовлетворяющих условию (7.3), т. е. точек преломляющей границы, определяются путем линейной интерполяции.

Ординаты Zгp точек преломляющей границы определяются по формуле:

Zгр=0,5 (U+V),

где U и V – параметры кубического сплайна, аппроксимирующего изохроны.

Интервальная граничная скорость определяется по формуле

где ∆t – шаг по времени изохрон.

Могут быть также построены временные динамические разрезы МПВ путем трансформации сейсмозаписей в шкалу времен t0 способами редуцирования и общей глубинной точки (площадки).

Наиболее характерными особенностями этих способов являются органическое объединение этапов обработки и интерпретации в одном алгоритме, не позволяющее их разграничить, и высокая степень автоматизации всего процесса перехода от полевых сейсмозаписей к временному сейсмическому разрезу, а также его технологичность.

Предшествующие построению преломляющих границ традиционные операции разделения, отождествления и корреляции волн заменены при построении временных разрезов анализом результативных сейсмозаписей, получаемых при переборе значений скорости (скоростным анализом).

Трансформация достигается путем ввода кинематических поправок, а при использовании многократных систем наблюдений – еще и путем суммирования получаемых в результате этой процедуры сейсмозаписей.

Уравнение годографа преломленной волны от горизонтальной преломляющей границы на глубине Н имеет вид:

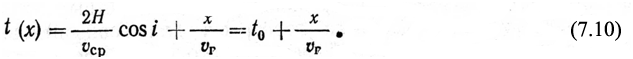
Из уравнения (7.10) следует, что t0 = t(x)–x/vг и кинематическая поправка δt, которую нужно ввести, чтобы трансформировать (редуцировать) годограф t(x) в линию t0:

Уравнение годографа преломленной волны от плоской наклонной границы может быть записано в виде:

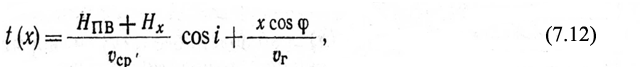
где HПВ и Нх – глубина до преломляющей границы соответственно на пункте возбуждения и пункте приема; φ – угол наклона преломляющей границы.

В этом случае

где vр – скорость редукции, численно равная кажущейся скорости vк встречного годографа преломленной волны.

В случае криволинейной преломляющей границы, переменной граничной скорости, а также латерального изменения скорости в покрывающей среде, величина скорости редукции меняется вдоль профиля и описанный упрощенный подход к определению кинематических поправок неэффективен.

Многократные системы наблюдений позволяют осуществлять более сложные алгоритмы редуцирования, которые накладывают меньшие ограничения на форму преломляющей границы и изменчивость граничной и средней скорости.

Уравнение годографа ОГТ для преломленной волны в случае плоской наклонной преломляющей границы, перекрытой однородной средой:

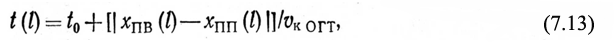
где l – длина базы наблюдений (расстояние между симметрично расположенными относительно точки ОГТ пунктами возбуждения и приема соответственно с координатами Хпв (l) ; vк ОГТ – кажущаяся скорость годографа ОГТ преломленной волны

где φ –угол наклона преломляющей границы.

Из уравнения (7.13) следует, что

Таким образом, кинематическая поправка, при введении которой годограф ОГТ преломленной волны трансформируется в горизонтальную линию на времени t0

Выражение (7.16) по форме тождественно выражению (7.11) и поэтому можно провести аналогию между величинами vкОГТ и vр. Отличие между двумя способами получения динамических временных разрезов состоит в том, что при редуцировании кинематические поправки вносятся в сейсмозаписи трасс ОПВ, а во втором способе поправки вносятся в сейсмозаписи трасс, отсортированные по ОГТ.

С целью выбора оптимального значения vкОГТ производят скоростной анализ. Для получения скоростных спектров в трассы сейсмограмм ОГТ вводятся кинематические поправки, рассчитываемые по формуле (7.16) для перебираемых с определенным шагом значений vкОГТ, которые затем суммируются. Искомому значению vкОГТ соответствует максимальная интенсивность суммарных колебаний.

С учетом присущих способам редуцирования и ОГТ ограничений динамические временные разрезы целесообразно использовать для построений, не требующих высокой точности результатов, или, когда имеются благоприятные сейсмогеологические условия, при выявлении высокоамплитудных объектов, размеры которых превышают максимальное расстояние взрыв–прибор.

Что касается возможностей и эффективности сейсмической томографии по первым вступлениям преломленных (рефрагированных) волн, то, так как томографический подход требует для обеспечения необходимой детальности и точности сейсмических построений использование при полевых работах очень плотных систем наблюдений он, как отмечалось выше, в основном используется при интерпретации данных малоглубинных работ МПВ, а также при определении априорных статических поправок по первым вступлениям преломленных волн на сейсмозаписях, получаемых при работах МОГТ.

Системы наблюдений, используемые при стандартных работах методом преломленных волн, этому условию не удовлетворяют. Требуемое для реализации томографического подхода существенное уменьшение расстояния между пунктами возбуждения практически не реализуемо, так как приводит к значительному удорожанию работ МПВ. В этом отношении морские сейсмические съемки более эффективны в ценовом отношении при использовании сейсмической томографии.

Если не вдаваться в детали, то сейсмическая томография реализуется следующим образом. Модель среды представляется в виде сетки, для ячеек или узлов которой задаются значения скорости. Через эту модель численными методами осуществляется трассировка сейсмических лучей, для которых определяются значения времен пробега. Эти рассчитанные значения затем сравниваются с наблюденными, и по расхождениям времен пробега итеративным путем корректируются значения скорости в ячейках (узлах) сетки до тех пор, пока эти расхождения не станут минимально возможными.

Следует отметить, что достоверность и точность результатов томографии, помимо полноты и плотности использованной системы наблюдений, зависит от качества корреляции первых вступлений и правдоподобности исходной скоростной модели.